Table of Contents
Bạn đang tìm hiểu về tâm đường tròn ngoại tiếp tam giác và muốn biết nó được xác định như thế nào? Bài viết này sẽ giải đáp chi tiết câu hỏi “tâm đường tròn ngoại tiếp tam giác là giao của ba đường gì” và cung cấp thêm những kiến thức quan trọng liên quan.
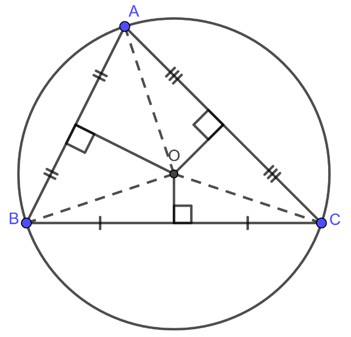Vẽ đường tròn ngoại tiếp của tam giác
Định nghĩa đường tròn ngoại tiếp tam giác
Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác đó. Tâm của đường tròn ngoại tiếp tam giác chính là giao điểm của ba đường trung trực của ba cạnh tam giác.
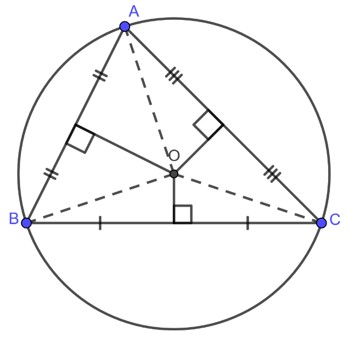Hình ảnh cụ thể về đường tròn ngoại tiếp của tam giác
Khoảng cách từ tâm đường tròn đến ba đỉnh của tam giác bằng nhau và chính là bán kính của đường tròn ngoại tiếp tam giác.
Tính chất của đường tròn ngoại tiếp tam giác
Dưới đây là một số tính chất quan trọng của đường tròn ngoại tiếp tam giác:
- Mỗi tam giác chỉ có duy nhất một đường tròn ngoại tiếp.
- Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác.
- Trong tam giác vuông, tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền.
- Trong tam giác đều, tâm đường tròn ngoại tiếp trùng với tâm đường tròn nội tiếp.
Một số kiến thức khác về đường tròn ngoại tiếp tam giác
Cách vẽ đường tròn ngoại tiếp tam giác
Để vẽ đường tròn ngoại tiếp tam giác ABC:
- Vẽ tam giác ABC.
- Vẽ đường trung trực của ba cạnh AB, BC, CA. Giao điểm của ba đường trung trực này chính là tâm I của đường tròn ngoại tiếp.
- Vẽ đường tròn tâm I, bán kính IA (hoặc IB, IC).
Cách xác định tâm đường tròn ngoại tiếp tam giác
Có hai cách xác định tâm đường tròn ngoại tiếp tam giác:
Cách 1: Gọi I(x;y) là tâm đường tròn ngoại tiếp tam giác ABC. Vì IA = IB = IC = R (R là bán kính), ta có hệ phương trình:
IA² = IB²
IA² = IC²
Giải hệ phương trình này để tìm tọa độ điểm I.
Cách 2: Viết phương trình hai đường trung trực của hai cạnh bất kỳ của tam giác. Giao điểm của hai đường trung trực này chính là tâm đường tròn ngoại tiếp tam giác.
Lưu ý: Đối với tam giác vuông, tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền.
Cách tính bán kính đường tròn ngoại tiếp tam giác
Bán kính đường tròn ngoại tiếp tam giác ABC với các cạnh a, b, c và diện tích S được tính theo công thức:
Công thức chi tiết để tính bán kính của đường tròn ngoại tiếp của tam giác
Phương trình đường tròn ngoại tiếp tam giác
Để viết phương trình đường tròn ngoại tiếp tam giác, ta thực hiện các bước sau:
- Thay tọa độ ba đỉnh của tam giác vào phương trình đường tròn tổng quát (x-a)² + (y-b)² = R², với (a,b) là tâm và R là bán kính.
- Giải hệ phương trình để tìm a, b, R.
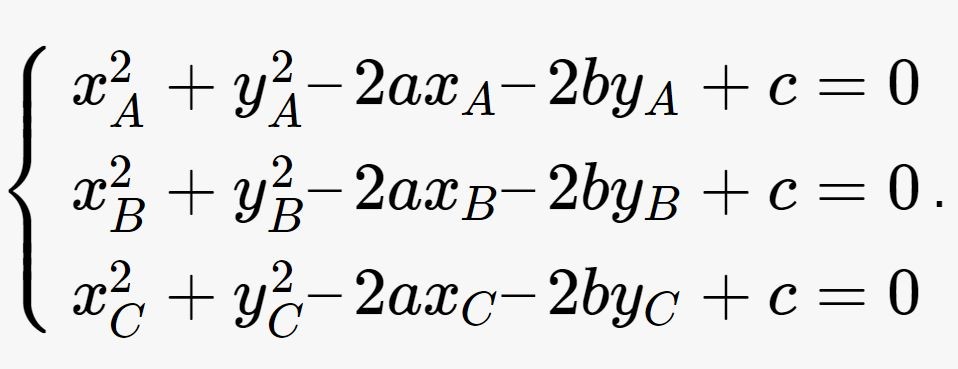Phương trình chi tiết của đường tròn ngoại tiếp của tam giác
Một số bài tập về đường tròn ngoại tiếp tam giác
Bài 1: Viết phương trình đường tròn ngoại tiếp tam giác ABC biết A(-1;3), B(5;1), C(-2;3).
Bài 2: Cho tam giác ABC với A(1;3), B(-1;1), C(2;2). Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
Bài 3: Cho tam giác ABC đều cạnh 8cm. Xác định bán kính và tâm đường tròn ngoại tiếp tam giác ABC.
Bài 4: Cho tam giác ABC đều cạnh 10cm. Xác định bán kính và tâm đường tròn ngoại tiếp tam giác ABC.
Bài 5: Cho tam giác ABC vuông tại A, AB=6cm, BC=8cm. Xác định tâm và bán kính đường tròn ngoại tiếp tam giác ABC.
Bài 6: Cho tam giác MNP có ba góc nhọn nội tiếp đường tròn (O;R). Ba đường cao MF, NE, PD cắt nhau tại H. Chứng minh tứ giác NDEP là tứ giác nội tiếp.
Nguồn: http://shininghome.edu.vn/ Tác giả: Nguyễn Lân dũng
Giáo sư Nguyễn Lân Dũng là một nhà khoa học tiêu biểu của Việt Nam trong lĩnh vực vi sinh vật học, với hơn nửa thế kỷ gắn bó với công tác giảng dạy và nghiên cứu (). Ông sinh trưởng trong một gia đình có truyền thống hiếu học, là con trai của Nhà giáo Nhân dân Nguyễn Lân. Trong suốt sự nghiệp, Giáo sư đã đảm nhận nhiều vai trò quan trọng như Chủ tịch Hội các ngành Sinh học Việt Nam, Đại biểu Quốc hội và được vinh danh với danh hiệu Nhà giáo Nhân dân vào năm 2010.